整数集合分割問題は、整数の集合 S を要素の総和が等しい2つの集合に分割する問題である。
例
$$S = \left\{ 1, 2, 3, 4 \right\} \rightarrow S_{1} = \left\{ 1, 4 \right\},
S_{2} = \left\{ 2, 3 \right\}$$
Hamiltonian:
$${\cal H} = A \left( \sum _{i=1} ^{N} n_{i} \sigma _{i} \right) ^{2} , \quad
\sigma _{i} \in \left\{ -1, 1 \right\}$$
具体的な解法
例) N=4(以下の集合)のケースを具体的に解いてみる。
$$S = \left\{ 1, 2, 3, 4 \right\} \rightarrow S_{1} = \left\{ 1, 4 \right\},
S_{2} = \left\{ 2, 3 \right\}$$
以下の手順を踏む。
- \( \sigma = \{ -1, 1 \}\)を\(q = \{ 0, 1 \}\)に置き換えて、QUBO形式に変換する
- QUBO形式を、一般的なHamiltonianの形式に変換する
- qsolvを使って解く
$${\cal H} = A \left( \sum _{i=1} ^{N} n_{i} \sigma _{i} \right) ^{2}
\rightarrow{}(\sigma_{1} + 2\sigma _{2} + 3\sigma _{3} + 4\sigma _{4}) ^{2}$$
$$N = 4, \quad n_{i} \in \left\{ 1, 2, 3, 4 \right\}$$
$$\sigma _{i} = 2q_{i} - 1$$
計算過程
Hamiltonianが最小値を取るスピン配置を求めることが目的なので、定数項(下式の場合は最後の”+100”)は無視する。
$${\cal H} = (\sigma _{1} + 2\sigma _{2} + 3\sigma _{3} + 4\sigma _{4})^{2}$$
$$= \left[ (2q_{1} - 1) + 2(2q_{2} - 1) + 3(2q_{3} - 1) + 4(2q_{4} - 1)\right]^{2}$$
$$= 4q_{1} ^{2} + 16q_{1}q_{2} + 24q_{1}q_{3} + 32q_{1}q_{4} - 40q_{1}$$
$${55pt}+ 16q_{2} ^{2} + 48q_{2}q_{3} + 64q_{2}q_{4} - 80q_{2}$$
$$+ 36q_{3} ^{2} + 96q_{3}q_{4} - 120q_{3}$$
$$+ 64q_{4} ^{2} - 160 q_{4} + 100$$
$$= 4\left( 4q_{1}q_{2} + 6q_{1}q_{3} + 8q_{1}q_{4} + 12q_{2}q_{3} +
16q_{2}q_{4} + 24q_{3}q_{4} \right)$$
$$ - 4\left( 9q_{1} + 16q_{2} + 21q_{3} + 24q_{4} \right)$$
$$ + 100$$
$$q_{i}^{2} = q_{i} , \quad q_{i} \in \left\{ 0, 1 \right\}$$
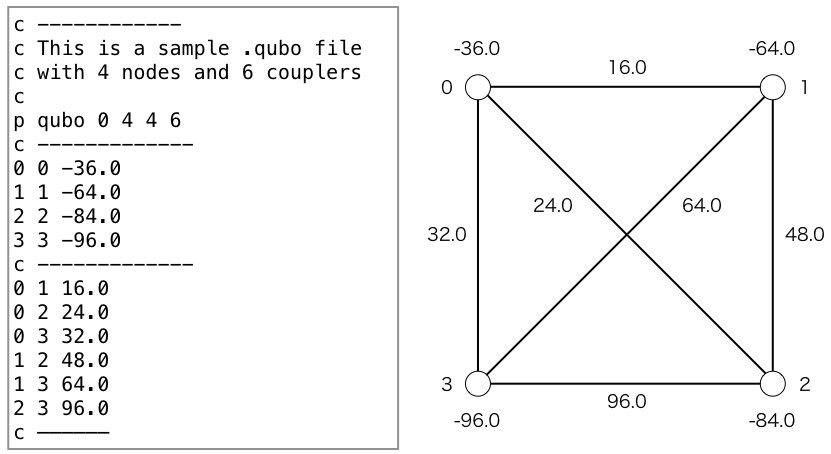
QUBO input file
qbsolv実行結果
期待する結果(以下)になっている。
※D-Waveを使っているわけではなく、シミュレータによる計算結果が出力される。
$$S = \left\{ 1, 2, 3, 4 \right\} \rightarrow S_{1} = \left\{ 1, 4 \right\},
S_{2} = \left\{ 2, 3 \right\}$$