量子アニーリング
量子コンピューティングは量子力学的な特徴を活かし、並列計算を実現する。量子コンピューティングの方式には、大別して「アニーリング」方式と「ゲート」方式の2つがある。本サイトでは、主に組合せ最適化問題に特化した「アニーリング」方式について説明する。
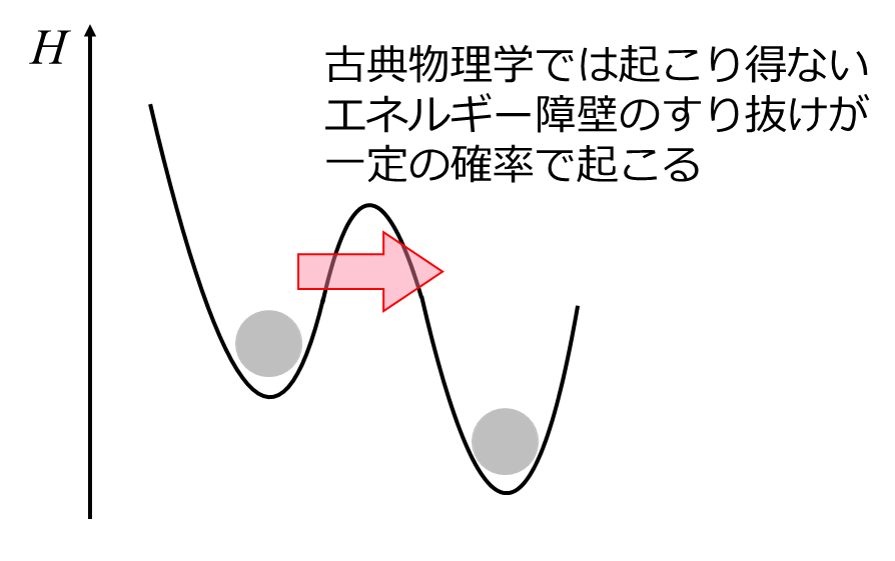
量子アニーリング方式は、イジングモデルと呼ばれる電子間の相互作用を記述するモデルを応用する。
イジングモデル(エネルギー):
スピンがメモリの「0/1」に対応する。イジングモデルのエネルギーが最小になるスピン配置が計算結果に対応する。
量子アニーリング方式は、「組合せ最適化問題」と呼ばれるタイプの問題解決に特化しており、汎用性はない。また、原理的に「最適解が存在する」問題であっても、解に到達しない可能性がある。
最適化問題を解くための流れ
- 問題の定式化を行う(問題を以下の形式で記述する)
$$H = sum _{i} h_{i} q_{i} + sum _{i , j} J_{i,j} q_{i} q_{j} ,, , quad qin { 0, 1 }$$
$$H = sum _{i} h_{i} q_{i} + sum _{i , j} J_{i,j} q_{i} q_{j}$$ $$ ,, , quad qin { 0, 1 }$$
- インプットファイルの作成を行う
- インプットファイルをqbsolvに入力して問題を解かせる
- 必要に応じて、アウトプットの解析を行う
※D-Wave社のQUBOのソルバqbsolvを使用した手順になる。
具体的な解き方について、組合せ最適化問題(整数集合分割問題、ナンバープレース問題)を参照する。
高次問題への対応
最適化問題をアニーリングマシンで解くときには、イジングモデルまたはQUBOに変換する必要がある。
q_{i} in left{ 0, 1 right}$$
q_{i} in left{ 0,1 right}$$
問題によっては、QUBO形式では記述できないケースがある。2次式よりも次数を高くしなければならないケースがある。
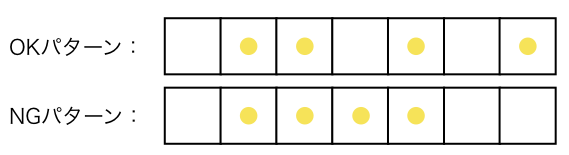
例)4日連続勤務を禁止する制限つきの勤務表作成
$$H_{add} = sum _{i} q_{i} q_{i+1} q_{i+2} q_{i+3}$$
すべてのQUBO変数が1のときに、エネルギーが上昇する(=ペナルティ)。
3次式をQUBO形式に変換する
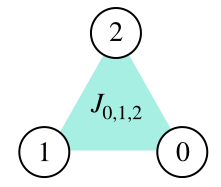
- 以下のハミルトニアン(3次式)を考える。
イジングモデルのハミルトニアン(QUBO形式)に変換する必要がある。
$$H = J_{0,1,2} ,q_{0} q_{1} q_{2}, quad q_{i} in { 0, , 1 }$$
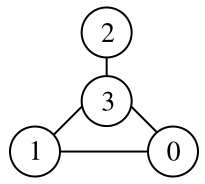
- ノード数を増やし新たな制約条件を付け加えることにより、3次式を2次式に変換する。
擬似的なノードを追加
変数(q_{3})を以下で定義する。
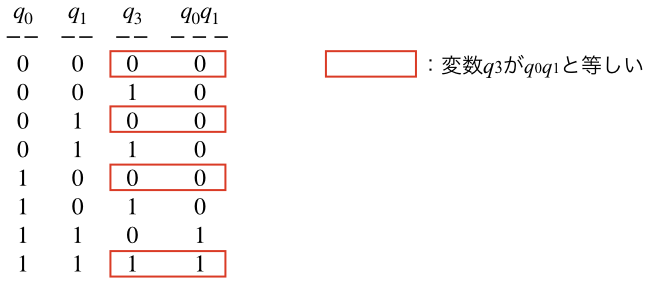
$$q_{0} q_{1} equiv q_{3}$$
これにより、擬似的に2変数の積に書き下すことができる。
$$q_{0} q_{1}q_{2} equiv q_{3} q_{2}$$
制約条件の追加
変数(q_{3})に制約条件を付け加える必要がある。変数(q_{3})が(q_{0}q_{1})と等しいときに、エネルギーが小さくなるようにハミルトニアンを構成する。
ハミルトニアン(最終形)
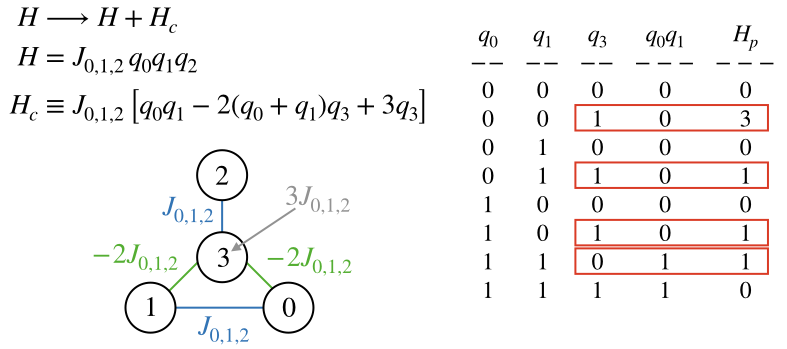
ハミルトニアンに制約条件の式を付け加えて、以下のようなハミルトニアンを採用する。変数(q_{3})が(q_{0}q_{1})と等しくないときには、エネルギーが上昇しペナルティとなる。
高次問題対応の基本的な手順
- 擬似的にノードを追加することで、3次以上の多項式をQUBO形式のハミルトニアンに帰着させる。
- 制約条件を課したハミルトニアンは以下のように書く。
q_{1}) q_{3} + 3 q_{3} right]$$
q_{1}) q_{3}$$ $$+ 3 q_{3} right]$$
制約条件のハミルトニアン:(q_{0} q_{1} - 2 (q_{0} + q_{1}) q_{3} + 3 q_{3} )
- 4次、5次…についても、同様の処置によってQUBO形式に帰着する。
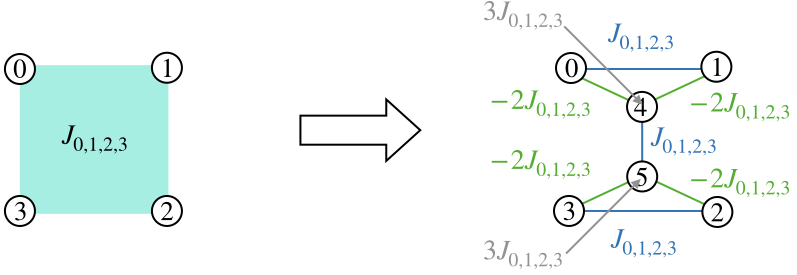
例)4次式の分解
$$H = J_{0, 1, 2, 3} ,q_{0}q_{1}q_{2}q_{3} equiv J_{0,1,2,3} , q_{4} q_{5}$$
$$H longrightarrow H + H_{c}^{(1)} + H_{c} ^{(2)}$$
$$H_{c}^{(1)} = J_{0, 1, 2, 3} left[ q_{0}q_{1} - 2 (q_{0} + q_{1}) q_{4} +
3q_{4}right]$$
$$H_{c}^{(2)} = J_{0, 1, 2, 3} left[ q_{2}q_{3} - 2 (q_{2} + q_{3}) q_{5} +
3q_{5}right]$$
量子アニーリング(量子コンピューティング)に関するお問い合わせについてはこちらをご覧ください。