ナンバープレースとは
3×3のブロックに区切られた9×9のマス目に、ルールに従って1から9の数字を埋めていくパズルゲームである。
量子アニーリングシミュレータ(qbsolv)でナンバープレース問題を解く方法について解説する。
ルール
- 縦横の各行列には、同じ数字を埋めてはならない
- 太枠で囲んだ3×3のマスに、同じ数字を埋めてはならない
QUBO変数の設定
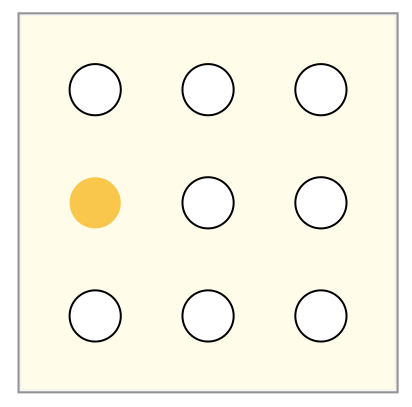
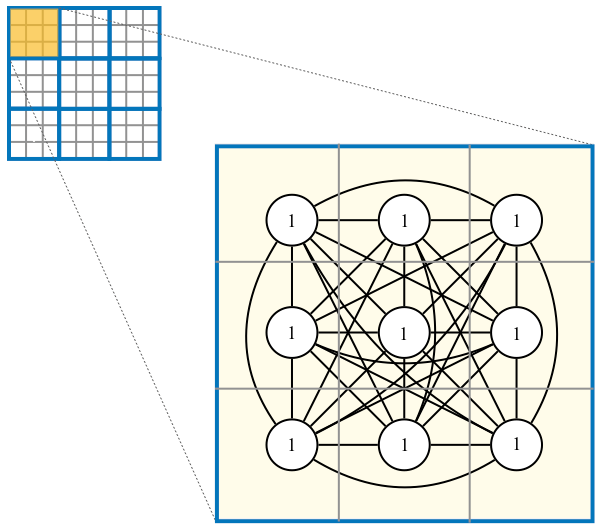
- 以下のようにxおよびyに1~9のインデックスを設定する
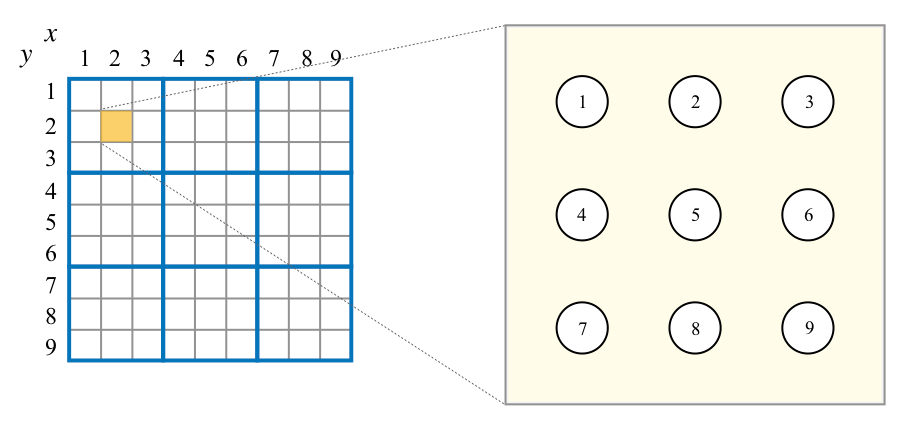
- 1~9の数字に対応させるために、各マスに9個、合計9×9×9=729個のQUBO変数を配置する
- QUBO変数のインデックスkは、座標(x, y)および数字nと対応付けられる。
例) 座標(x, y)に4を埋める場合、QUBO変数は以下の通り
$$q_{x, y, 1} \equiv q_{81(y-1)+9(x-1) + (1-1)} = 0$$
$$q_{x, y, 2} \equiv q_{81(y-1)+9(x-1) + (2-1)} = 0$$
$$q_{x, y, 3} \equiv q_{81(y-1)+9(x-1) + (3-1)} = 0$$
$$q_{x, y, 4} \equiv q_{81(y-1)+9(x-1) + (4-1)} = 1$$
$$q_{x, y, 5} \equiv q_{81(y-1)+9(x-1) + (5-1)} = 0$$
$$q_{x, y, 6} \equiv q_{81(y-1)+9(x-1) + (6-1)} = 0$$
$$q_{x, y, 7} \equiv q_{81(y-1)+9(x-1) + (7-1)} = 0$$
$$q_{x, y, 8} \equiv q_{81(y-1)+9(x-1) + (8-1)} = 0$$
$$q_{x, y, 9} \equiv q_{81(y-1)+9(x-1) + (9-1)} = 0$$
定式化のための命名
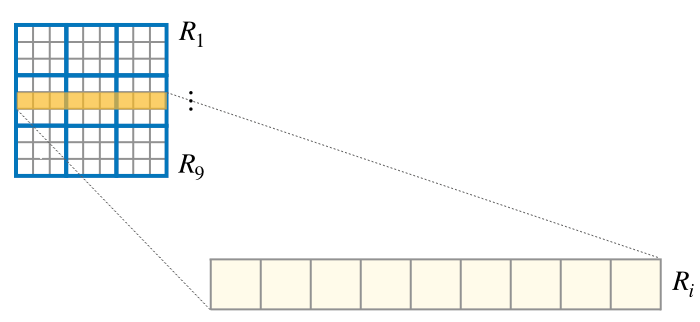
定式化のために、行、列、3x3領域に名前をつける。- \(行 : R_{i}\)
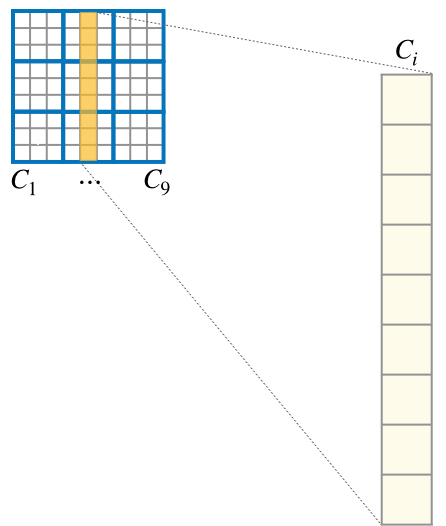
- \(列 : C_{i} \hspace{20pt} i \in \{ 1, 2, \cdots, 9 \}\)
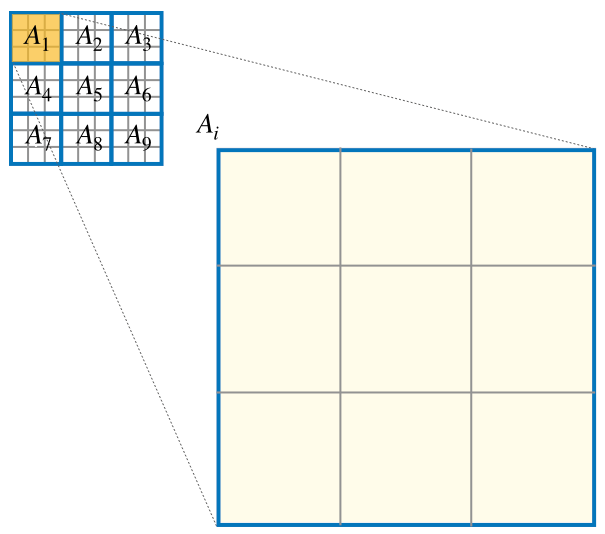
- \(3x3領域 : A_{i}\)
定式化のための命名(行)
定式化のための命名(列)
定式化のための命名(3x3領域)
イジングモデル
数独のルール(制約条件)を定式化する。
$$H = \sum _{x=1} ^{9} \sum _{y=1} ^{9} H_{1} ^{(x, y)} + \sum _{n=1} ^{9}
\sum _{i=1} ^{9} H_{2} ^{(i, n)}$$
$$H_{1} ^{(x,y)} = \left( 1 - \sum _{n=1} ^{9} q_{x,y,n} \right) ^{2}
\longrightarrow -\sum _{n=1} ^{9} q_{x,y,n}+ \sum _{n=1} ^{8} \sum
_{m=n+1} ^{9} q_{x,y,n} q_{x,y,m}$$
$$H_{2} ^{(i, n)} = \left[ \sum _{(x, y),(x^{\prime}, y^{\prime}) \in R_{i}}
+ \sum _{(x, y),(x^{\prime}, y^{\prime}) \in C_{i}} + \sum _{(x, y),
(x^{\prime}, y^{\prime}) \in A_{i}} \right] q_{x, y, n} q_{x^{\prime},
y^{\prime}, n}$$
QUBO変数の設定に基づく制約条件
各マスに設定されたQUBO変数は、必ず1つだけ1でなければならない。 $$H_{1} ^{(x,y)} \longrightarrow -\sum _{n=1} ^{9} q_{x,y,n} + \sum _{n=1} ^{8} \sum _{m=n+1} ^{9} q_{x,y,n} q_{x,y,m}$$x数独のルールに基づく制約条件
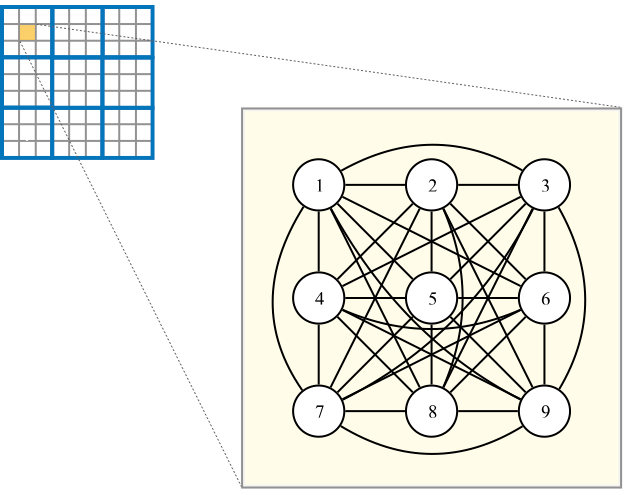
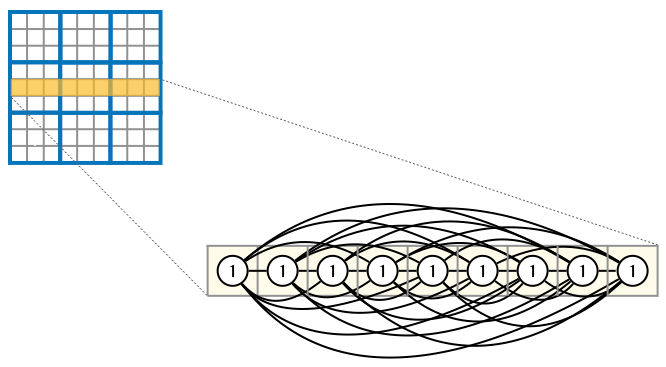
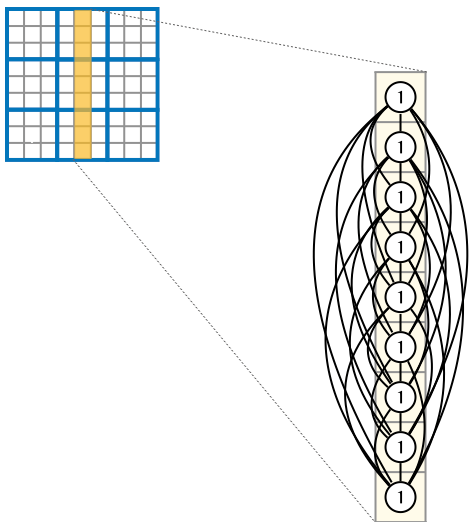
各行、列、3×3領域では、同じ数字が重複してはならない。
$$H_{2} ^{(i, n)} = \left[ \sum _{(x, y),(x^{\prime}, y^{\prime}) \in R_{i}}
+ \sum _{(x, y),(x^{\prime}, y^{\prime}) \in C_{i}} + \sum _{(x, y),
(x^{\prime}, y^{\prime}) \in A_{i}} \right] q_{x, y, n} q_{x^{\prime},
y^{\prime}, n}$$
数独のルールに基づく制約条件(行)
数独のルールに基づく制約条件(列)
数独のルールに基づく制約条件(3x3領域)
イジングモデルのハミルトニアン
qbsolvが解けるモデルは以下のハミルトニアン形式で記述される。- 1次の係数(h)は、すべてのQUBO変数に対して-1
- 2次の係数(J)は、すべての結合に対して+1
特定のマスを固定する
実際の数独の問題は、特定のマスに予め数字が設定されている。 これをイジングモデルに反映させるためには、1次の係数を変更してやればよい。- 1次の係数を負の値にすれば、対応するQUBO変数は1になりやすい傾向を持つ
- パラメータの値は、他のパラメータとのバランスを考慮して決める必要がある。
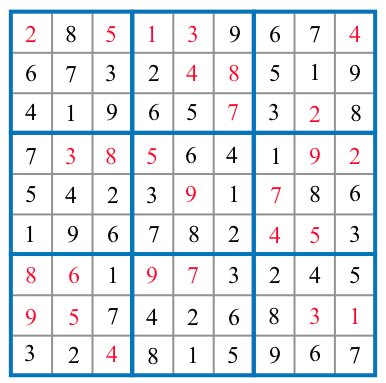
解答例(例題を解く)
以下の例題1) に適用。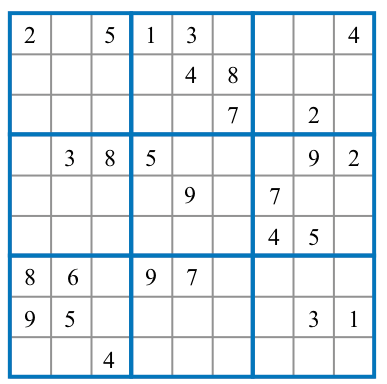
1) http://www.sudokugame.org/archive/printable.php?nd=4&y=2018&m=03&d=1
パラメータ調節
固定するマスに対応するパラメータ(h)は、-1から-5に変更する。- 確実にQUBO変数を1に固定するため
- -2で試した場合、期待する結果に収束しないケースがあった
結果
ナンバープレース問題(量子コンピューティング)に関するお問い合わせについてはこちらをご覧ください。